Flat vector bundle
In mathematics, a vector bundle is said to be flat if it is endowed with a affine connection with vanishing curvature, ie. a flat connection.
Contents |
de Rham cohomology of a flat vector bundle
Let 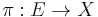 denote a flat vector bundle, and
denote a flat vector bundle, and 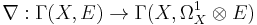 be the covariant derivative associated to the flat connection on E.
be the covariant derivative associated to the flat connection on E.
Let 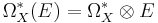 denote the vector space (in fact a sheaf of modules over
denote the vector space (in fact a sheaf of modules over 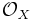 ) of differential forms on X with values in E. The covariant derivative defines a degree 1 endomorphism d, the differential of
) of differential forms on X with values in E. The covariant derivative defines a degree 1 endomorphism d, the differential of 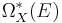 , and the flatness condition is equivalent to the property
, and the flatness condition is equivalent to the property 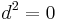 .
.
In other words, the graded vector space 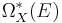 is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.
is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.
Flat trivializations
A trivialization of a flat vector bundle is said to be flat if the connection form vanishes in this trivialization. An equivalent definition of a flat bundle is the choice of a trivializing atlas with locally constant transition maps.
Examples
- Trivial line bundles can have several flat bundle structures. An example is the trivial bundle over
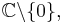 with the connection forms 0 and
with the connection forms 0 and 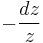 . The parallel vector fields are constant in the first case, and proportional to local determinations of the complex logarithm in the second.
. The parallel vector fields are constant in the first case, and proportional to local determinations of the complex logarithm in the second.
- The real canonical line bundle
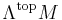 of a differential manifold M is a flat line bundle, called the orientation bundle. Its sections are volume forms.
of a differential manifold M is a flat line bundle, called the orientation bundle. Its sections are volume forms.
- A Riemannian manifold is flat if, and only if, its Levi-Civita connection gives its tangent vector bundle a flat structure.
See also
- Vector-valued differential forms
- Local system, the more general notion of a locally constant sheaf.
- Orientation character, a characteristic form related to the orientation line bundle, useful to formulate Twisted Poincaré duality
- Picard group whose connected component, the Jacobian variety, is the moduli space of algebraic flat line bundles.
- Monodromy, or representations of the fundamental group by parallel transport on flat bundles.
- Holonomy, the obstruction to flatness.